5. Visualization
2024-01-21
BUGS!!!
I tried visualising the neural net outputs using matplotlib and I noticed the training data was all wrong!!! There were two bugs:
-
Board class is mutable... so when we ran
generate_random_game, the board state saved inhistorywould be only a pointer to the current board. So as the game progressed the history instead of looking like[(P0, M0), (P1, M1), ... (Pn, Mn)]would look like[(Pn, M0), (Pn, M1), ... (Pn, Mn)]. -
In
chess_utils.py,moves_to_tensor, I had assumed thattorch.BoolTensorwould give me a tensor with allFalsein the beginning. That was incorrect, it instead gives me a tensor filled withTrueandFalserandomly. (Probably garbage values because we didn't initialise the buffer with anything). So we had to usetorch.zerosinstead.
Bug fixes:
def generate_random_game() -> List[Tuple[chess.Board, List[chess.Move]]]:
board = chess.Board()
history = []
while not board.is_game_over():
# print(board)
valid_moves = list(board.generate_legal_moves())
# print(valid_moves)
random_move = random.choice(valid_moves)
+ history.append((chess.Board(board.fen()), valid_moves))
- history.append((board, valid_moves))
board.push(random_move)
return history
def moves_to_tensor(moves: List[chess.Move]) -> torch.Tensor:
+ moves_tensor = torch.BoolTensor(64*64)
- moves_tensor = torch.zeros(64*64)
valid_actions = [move_to_action(move) for move in moves]
moves_tensor[valid_actions] = 1
return moves_tensor
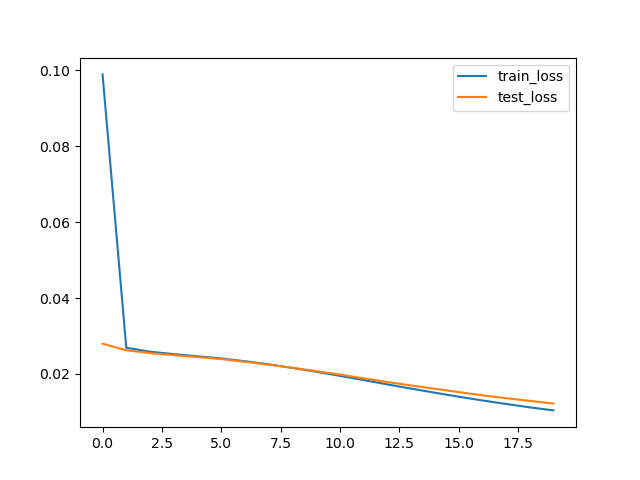
After fixing these two bugs, the neural nets started training much better!
Before bug fix:
run_num,OPTIMIZER,NUM_TRAINING_EXAMPLES,BATCH_SIZE,NUM_EPOCHS,LEARNING_RATE,final_train_loss,final_test_loss,running_time
1,ADAM,10000,128,20,1,0.0917012087764248,0.0948999347165227,9.442247152328491
After bug fix:
run_num,OPTIMIZER,NUM_TRAINING_EXAMPLES,BATCH_SIZE,NUM_EPOCHS,LEARNING_RATE,final_train_loss,final_test_loss,running_time
1,ADAM,10000,128,20,1,0.010415336841510402,0.012209153734147549,9.533048629760742
Visualizations
Ok, after training the network again let's now look at the visualizations again. This is the code I used to visualise the networks:
# To plot the board tensor
def plot_pos_tensor(tensor: torch.Tensor):
fig, axs = plt.subplots(1, 7, figsize=(15, 5))
channel_names = ['TURN', 'PAWN', 'KNIGHT', 'BISHOP', 'ROOK', 'QUEEN', 'KING']
for i in range(7):
axs[i].imshow(tensor[i, :, :], cmap='gray', vmin=-1, vmax=1, origin="lower")
axs[i].set_title(channel_names[i])
plt.show()
# To plot the moves tensor
# This will plot the moves tensor of length 4096 as a 64x64 image.
# The image can be thought of as a big chessboard with small chessboards on
# each square. The bigger square represents the start square and the smaller
# square represents the end square for each move.
def plot_move_set(moves: torch.Tensor):
moves_view = torch.zeros(64, 64)
for start_row in range(8):
for start_col in range(8):
for end_row in range(8):
for end_col in range(8):
action_num = (start_row+start_col*8)*64+(end_row+end_col*8)
moves_view[start_col*8+end_col][start_row*8+end_row] = moves[action_num]
plt.imshow(moves_view, origin="lower", vmin=0, vmax=1)
plt.show()
# To plot the top k moves as arrows on an svg chess board
# (use in jupyter notebooks)
# The opacity of the arrow is proportional to the move probability.
def plot_board_moves(board: chess.Board, probs: torch.Tensor, k=20):
arrows = []
probs, actions = torch.topk(probs, k)
for prob, action in zip(probs, actions):
arrow_color = f"#009900{int(prob*128):02x}"
move = action_to_move(action.item(), board)
print(move, prob)
arrows.append(chess.svg.Arrow(move.from_square, move.to_square, color=arrow_color))
return chess.svg.board(board, arrows=arrows)
Start position
Here's what the start position looks like:

And here is a representation of the valid moves of the start position:
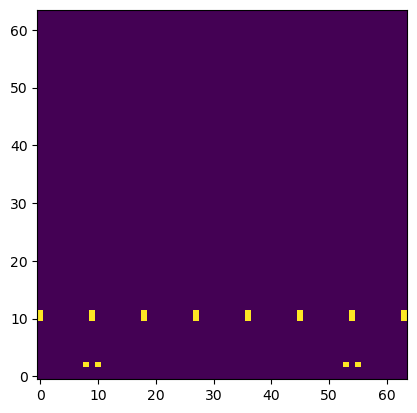
Note that this is a 64x64 image and it can be thought of as a big chessboard with small chessboards on each square. The bigger square represents the start square and the smaller square represents the end square for each move.
We can see the pawns having 2 moves each and the knights also having 2 possible moves each in the starting position. All other pieces are blocked.
Position 1
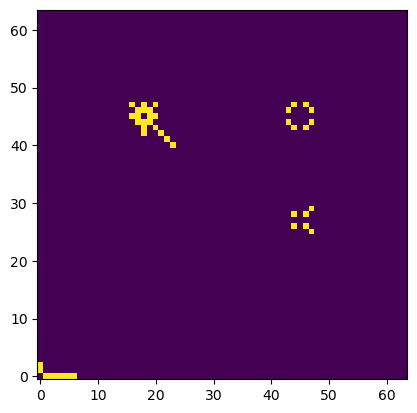
Let's look at a certain random position. It's Black's turn to play.

This should be the correct answer for the possible moves:
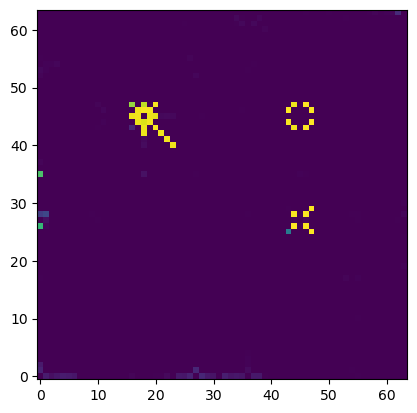
And if we plot what the neural network outputs, this is what we get (the predicted probabilities for the possible moves):
Here's how it looks like represented on a chessboard with arrows. (The opacity of the arrow is proportional to move probability.)
We can see its mostly correctly predicting the moves for the queen and bishop, although it's still predicting a bit of probability for the black bishop going past the white bishop. It's also struggling a bit to predict the rook moves which are totally valid (not sure why) but there is still some probability predicted for those. Also the black king shouldn't be able to move anywhere (check), and the net definitely is showing low probabilities for those moves.
So the net definitely understands some sort of concept that the king can't move into check.
Position 2
Here's another slightly trickier position. This time it's tricky to predict the right moves because the king is in check and there is really only one move that is valid in this position (bishop to d2 to block the check).
Board tensor:

Valid moves (only one pixel is ON):
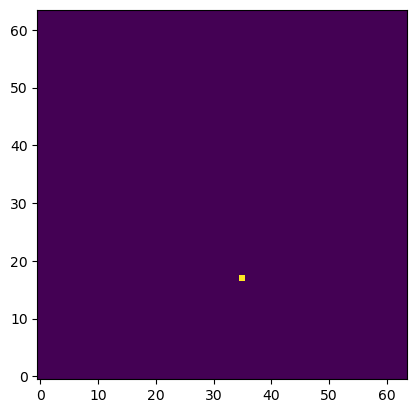
This is what the neural net predicts:
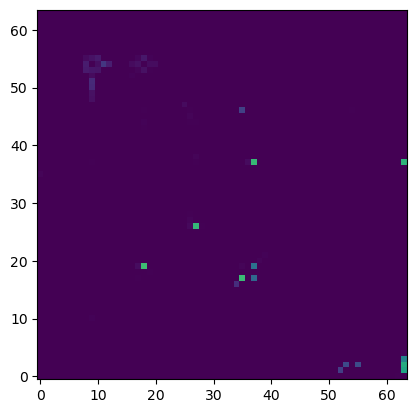
Here are the raw probabilities for each move:
c3c4 tensor(0.6879)
e3d2 tensor(0.6831)
e5f6 tensor(0.6757)
d4d3 tensor(0.6654)
h5h6 tensor(0.6511)
h1h3 tensor(0.6164)
h1h2 tensor(0.5898)
h1h4 tensor(0.4512)
e3f4 tensor(0.3785)
e3f2 tensor(0.3347)
The correct move is e3d2, it has the second highest probability. However the net is still struggling to understand this position (as I would have expected). It is only a single layer net so far, probably more layers would be required to understand how to detect (and block) checks. Intuitively, it takes one mental step to generate valid moves, it takes one more step to detect checks, and yet one more step to realise that we are in check and we need to block it.
Anyway, I've committed the code so far at commit a7f6106. Make sure to check out
the visualisations in the jupyter notebook!.
Okay so what next? Next I'll try to develop an evaluation framework to (a) test the network by 'live' play and measure number of moves played, (b) measure metrics like precision/recall (c) Try more neural net architectures to drive those metrics up!